אקסיומת השלמות

1 מהו שטח?

$\mathrm{♣}$

לפני שאוכל להמשיך אצטרך להסביר למה אני מתכוון שאני מדבר על "הזחה"1לא מצאתי שום מקור שמדבר על "הזחה" באופן דומה, קרוב לוודאי שקראתי ספר יחיד שדיבר בשפה זו או שהמצאתי את המושג בעצמי. ולשם כך אתן כמה דוגמאות:

1. ישר הוא הזחה של נקודה בשיפוע קבוע
2. מלבן הוא הזחה של קטע אחד לאורך קטע אחר המאונך לו
3. מקבילית היא הזחה של ישר אחד לאורך קטע אחר ללא תלות בזווית שביניהם ובלבד שלא יהיו מקבילים
4. עיגול הוא הזחה של "מחוג" באורך הרדיוס של העיגול כשאחד מקצותיו נותר קבוע במקומו והאחר מסתובב סביבו סיבוב שלם
5. תיבה היא הזחה של מלבן לאורך קטע המאונך למישורים שבהם עובר המלבן בתהליך ההזחה
6. פירמידה היא הזחה של מצולע לאורך קטע המאונך לו כאשר המצולע קטן ביחס ישר למרחק שנשאר עד לסיום ההזחה

$$

כלומר הזחה של צורה (קבוצת נקודות כלשהי) במרחב לאורך עקומה כלשהי היא קבוצת כל הנקודות שהצורה "עוברת" בהן שמזיזים אותה לאורך העקומה.

$\mathrm{♣}$

לא מדובר במושג מתמטי מוגדר היטב (למרות שאולי ניתן לפרמל אותו) וכפי שציינתי בהערה לא מצאתי אך אחד אחר שמדבר על הזחה באופן דומה.

2 איך מחשבים שטח של צורה נתונה?

3 מה הקשר בין שטח לאינטגרלים?

$\mathrm{♣}$

לו הייתי יכול להכניס את האנימציה הזו לקובץ PDF הייתי מוסיף אותה כאן שכן היא מסכמת את הנאמר בצורה נהדרת.

4 דוגמאות

$\mathrm{♣}$

אנחנו יודעים גם ששטח עיגול שרדיוסו הוא $r$ שווה ל-$4\cdot \underset{0}{\overset{r}{\int }}\sqrt{r^2-x^2}dx$ אך מכיוון ש-$\pi$ הוא מספר טרנסצנדנטי לא נוכל להציג את האינטגרל בצורה טובה יותר לעת עתה, זו הסיבה לכך שהתחלתי לחשב נפחים במקום להראות חישוב "בסיסי יותר" של שטח עיגול או אליפסה.

$\mathrm{♣}$

הנה ניסיון שלי בילדותי לקשר בין $\pi$ של היקף העיגול לבין $\pi$ של שטחו: ניקח "מחוג" באורך רדיוס העיגול ונזיח אותו כשאחד מקצותיו נותר קבוע במקומו והאחר מסתובב סביבו סיבוב שלם, א"כ כמו שחישבנו את שטח המלבן נקבל כעת ששטח העיגול הוא $2\pi r$ "פעמים" $r$, כלומר $2\pi r^2$! למה זה לא עובד? למה האינטואיציה של הוכחת התוספות הצליחה בעוד ששלי נכשלה?
ובכן התשובה ברורה: למה החלטתי שאורך העקומה שלאורכה אני מזיח את המחוג היא $2\pi r$? הרי בכל נקודה של המחוג אורך העקומה שונה! מכאן אנחנו למדים שהאינטואיציה עובדת באופן פשוט רק כאשר העקומה שלאורכה אנו מזיחים את הצורה המדוברת מאונכת לאותה צורה13מכיוון שהשטחים היחידים שאנחנו באמת יודעים לחשב הם של מלבנים ולפיהם הגדרנו את מושג השטח.; אחרת יש לבצע תיקונים, במקרה הזה התיקון הנדרש הוא חישוב ממוצע בין אורכי העקומות השונות שמרכיבות את המסלול של כל נקודה במחוג ומכיוון שאין שום סיבה להעדיף אחת מהן על פני חברתה הממוצע הוא בדיוק $\pi r$ אבל זה כבר ממש לא אינטואיטיבי ולא ברור שזה עובד ולכן כדאי להישאר עם האינטואיציה של הזחה במאונך לקטע המוזח.
אם בכל זאת רוצים לדעת כיצד לבצע תיקון ניתן להיעזר באינטואיציה הבאה: אם ניקח מקבילית שאינה מלבן ונזיח את אחת מצלעותיה לאורך אחת מהצלעות שאינה מקבילה לה נקבל את שטח המקבילית, אבל הכפלת אורכי הצלעות נותנת תשובה שגויה משום שהקטע המוזח אינו מאונך לקטע שלאורכו הוא מוזח; לכן צריך להכפיל את התשובה השגויה ב-$\sin \alpha$ כאשר $\alpha$ היא אחת הזוויות במקבילית (לא משנה איזו כי $\sin \alpha =\sin (\pi -\alpha )$) כדי לקבל מהקטע השגוי את הקטע הנכון. באותה דרך ניתן לתקן כל חישוב שבו הקטע השגוי בעל זווית קבועה בינו לבין הקטע הנכון לאורך כל ההזחה, אך לא מצאתי דרך לבצע את התיקון הזה באינטואיציה שלי עם המחוג מפני שלא מצאתי את הישר הנכון.

$\mathrm{♣}$

למיטיבי לכת: מיד לאחר ההסבר על הקשר בין היקף העיגול לשטחו התוספות עוברים להוכיח שמתקיים $1.4<\sqrt{2}$.

"...ואם באנו לכוין החשבון דמרובע יתר על העגול נוכל להוכיח בענין זה שתעשה נקודה של משהו (נקודה שאין לה שטח - עיגול קטן לאינסוף) ותקיפנה בחוטין הרבה סביב זה סיבוב אחר סיבוב עד שירחיבו ויגדל רוחב בעוגל טפח על טפח (עד שהקוטר יהיה באורך טפח ולכן הריבוע החוסם יהיה טפח על טפח); ואחר כך תחתך החוטין מן הנקודה ולמטה (ראו חלק מס' 1 באיור למטה), דהיינו מחצי רוחב עיגול ולמטה, ואחר שיחתכו יתפשטו כל החוטין מימין ומשמאל ונמצא כל חוט הולך ומאריך מחבירו משהו מכאן ומשהו מכאן עד שאתה מגיע לחוט העליון דארכו ג' טפחים שהוא חוט החיצון שהוא מסבב טפח על טפח דכל שיש ברוחבו טפח (כל עיגול שקוטרו באורך טפח) יש בהיקפו שלשה טפחים (היקפו הוא שלושה טפחים - הקירוב של $\pi$ שהגמרא והתוספות משתמשים בו הוא $3$). נמצאו החוטין הללו סדורין כענין זה: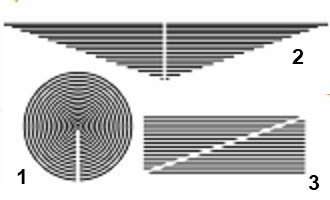

כמין רצועה רחבה באמצע חצי טפח, והיינו כנגד הנקודה, מכאן ומכאן כלה והולכת וצרה עד משהו (עד $0$, כלומר מדובר במשולש שווה שוקיים שאורך הבסיס שלו הוא $3$ טפחים ואורך הגובה שלו הוא $\frac{1}{2}$ טפח, ראו חלק מס' 2 באיור לעיל). ואם באת לחזור ולחלק אותה באמצע היינו כנגד הנקודה תמצא שתי רצועות שכל אחת ארכה טפח ומחצה ומצד אחת רחבה חצי טפח ומצד אחת כלה עד משהו (כלומר מדובר בשני משולשים ישרי זווית שאורך אחד מניצביו הוא $1\frac{1}{2}$ טפחים וארך האחר $\frac{1}{2}$ טפח, שוב החלק מס' 2), ועתה תצטרף אלו שתי הרצועות ושים הארוך כנגד הקצר את תמצא רצועה ארכה טפח ומחצה על רוחב חצי טפח (חבר את שני המשולשים זה לזה כך שייווצר מלבן שאורכי צלעותיו כאורכי הניצבים של שני המשולשים, ראו חלק מס' 3 באיור); תחלוק אותה לשלש רצועות תמצא בה שלש רצועות מחצי טפח על חצי טפח (נחלק את המלבן לשלושה ריבועים חופפים שאורך צלעותיהם הוא חצי טפח), ואילו רצועה מרובעת של טפח (ריבוע שאורך צלעותיו הוא טפח - שהוא הריבוע אליו אנו משווים את העיגול) כשתחלקנה שתי וערב תמצא בה ארבע רצועות של חצי טפח על חצי טפח הרי לך מרובע יתר על העיגול רביע."

$$$$$$$$

הסבר של דברי התוספות בשפה אינטואיטיביתניקח עיגול שקוטרו $2r$ נחתוך בו רדיוס ו"נפתח" את העיגול למשולש שווה שוקיים שאורך בסיסו כאורך היקף העיגול, והמרחק בין כל שתי נקודות הנמצאות באותו הגובה בשוקיים הוא כהיקף העיגול שאורך רדיוסו הוא המרחק בין הקטע שבין שתי הנקודות לבין הקודקוד שבין שתי השוקיים. הסיבה לכך שאכן קיבלנו משולש היא ההנחה שלנו שקיים יחס ישר בין היקף המעגל לקוטרו ולרדיוסו, ולכן הפונקציה המתאימה לכל נקודה על הרדיוס את היקף המעגל המתאים היא פונקציה ליניארית.
א"כ שטח העיגול הוא כשטח משולש שווה שוקיים שאורך בסיסו הוא $2\pi r$ וגובהו $r$, כלומר:$$\frac{2\pi r\cdot r}{2}=\pi r^2$$$$$$דברי התוספות - "צורת הדף"

lyxscale 40

מקור:

פורטל הדף היומי.

$$
אם נרצה להמיר את ההוכחה של התוספות לשפה האינטואיטיבית שדיברנו בה קודם אז נאמר שאנו לוקחים "מעגל" ברדיוס $0$ ומזיחים אותו לאורך רדיוס העיגול כך שהמעגל גדל בהתאם לרדיוס, הפונקציה המתארת את גודל המעגל כתלות ברדיוס היא הפונקציה $f\left(x\right)=2\pi x$ שהשטח מתחת לגרף שלה הוא משולש ישר זווית שאורך ניצבו האחד כאורך רדיוס העיגול ואורך ניצבו האחר הוא כהיקף העיגול ושוב קיבלנו את הנוסחה:$$\frac{2\pi r\cdot r}{2}=\pi r^2$$נשים לב לכך ש-$\int f\left(x\right)dx=\int 2\pi xdx=\pi x^2+C$ ולכן הפירמול של האינטואיציה הזו הוא באמירה ששטח העיגול הוא האינטגרל:$$\underset{0}{\overset{r}{\int }}2\pi xdx=\pi r^2-\pi \cdot 0^2=\pi r^2$$